You want to throw a ball straight up into the air so that it reaches a height of 3.3 m above the ground.
a) If the ball leaves your hand at a height of 1.2 m above the ground, how fast do you need to throw it?
b) How long does it take the ball to hit the ground? You may ignore any effects of air resistance throughout this problem.
-
In this problem, you are asked to describe the motion (how fast, how far, how long) of the ball. Whenever you are asked to describe the motion of an object without worrying about the cause of that motion, you have a kinematics problem.
-
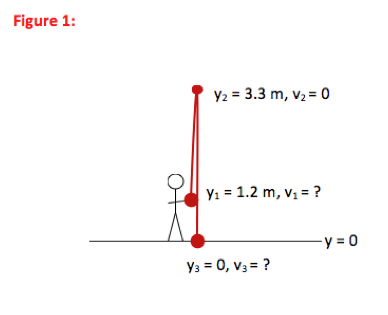
There are three key kinematic equations. If you carefully select the equation which most directly describes the situation in your problem, you will not only solve the problem in fewer steps but also understand it better. The three equations, written for motion in the y-direction, are:
1. y = y0 + v0Δt + ½ a(Δt)2 (relates position and time)
2. v = v0 + aΔt (relates velocity and time)
3. v2 = v02 + 2a(Δy) (relates velocity and position)
a) The initial velocity of the ball is a variable in all three equations, so this question drives home the point that there is more to selecting the appropriate relationship than just noting what value is requested in the problem. In this case, you want to find the starting velocity that gives a maximum height of 3.3 m. Maximum height is the position at which y-velocity is zero. The question relates position and velocity, so you want to use equation 3.
b) You are asked how long (time) it takes the ball to reach the ground (position), so you want to use equation 1.
-
Step 1:


The velocity when the ball left your hand (Point 1) is the information that was requested in part a) of the problem.
--------------------------------------------------------------------------------------------
Step 2:

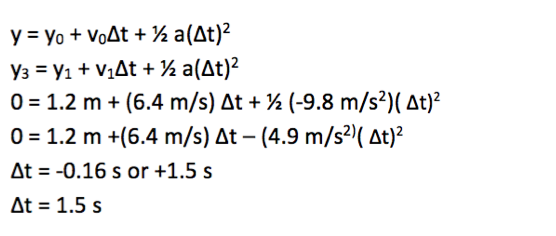
Part b) of the problem asked for the amount of time the ball was in the air (between Point 1 and Point 3.) No further mathematical solution is required.
The statement of the problem gave all vertical positions relative to the ground, so I chose the ground to be the y = 0 point.
The first point described in the problem is when the ball leaves your hand. At that point, the ball is 1.2 m above the ground, which was chosen to be the y = 0 reference point. You do not know how fast the ball is moving as it leaves your hand, and so v1 is unknown.
The ball rises to a height of 3.3 m above the ground, or 3.3 m above the y = 0 position. You also have information about velocity at this point. You know that gravity causes an object to slow down as it moves upward and speed up as it moves downward. At the top of the motion (the highest point), the vertical (or y) component of the object’s velocity is zero.
At the final point in the problem, the ball reaches the ground, or a height of zero. It is a very common mistake to assume that the velocity of the ball is zero at this point. But remember the kinematic equations only apply over periods of constant acceleration. As soon as the ball touches the ground, the ground causes it to slow down very quickly—it no longer has a downward acceleration of g. So Point 3 is the point just before the ball touches the ground.
In this case, the motion of the ball is strictly vertical. You only have y-direction motion. Therefore, you do not need to divide any of the variables into their x- and y-components.
I drew the motion of the ball as a parabola, rather than straight up and down, only so that I could clearly mark points 1, 2, and 3 on the drawing.The t in the kinematic equations refers to the time interval between the two points in the equation, with y0 occurring at the earlier time. I use Δt rather than t to be explicit that this is a time interval (t – t0) and not a point in time.
Some text books will give more than three kinematic equations—for example, they may provide “range equations” or different versions of the equations for horizontal and vertical motion. Those are just these three equations solved for special cases. In my view, it is better to know and understand three equations that will always work than to memorize many equations which are specific to certain situations only.You are asked to find the velocity of the ball at Point 1 (when it leaves your hand) in order for it to have the required motion at Point 2 (reaches a height of 3.3 m.) Therefore, “y0” and “y” are “y1” and “y2” respectively.
The acceleration of the ball (due to gravity) is downward, which is the negative y-direction as chosen in this problem. Because a, v, and y are all vector quantities, their values must be given a + or – sign to represent direction whenever they are filled into any of the kinematic equations.
Many of the most common mistakes in kinematic problems can be avoided with careful attention to book keeping. When we drew the picture, we were careful to label each point of interest with a different subscript, and when we fill into the equation we need to be careful to fill in the correct value for the correct point. We cannot assume that values of zero go with the earlier point in times. In this expression, in fact, the velocity of zero occurs at the top of the motion (Point 2) rather than at the start (Point 1.)
Only two significant figures were given in the text of the problem, so only two significant figures are included in the solution.
You are asked to find the amount of time the ball takes to get from Point 1 (when it leaves your hand) until it reaches the ground (Point 3.) Therefore, “y0” and “y” are “y1” and “y3” respectively.
To solve for Δt in this equation, recognize that you have a quadratic equation: it has the form a Δt2 + b Δt + c = 0, where a = -4.9, b = 6.4, and c = 1.2. (A quick look at units tells you that Δt must be in seconds, so I will not carry units through on the algebra to solve the quadratic equation, merely because I want to avoid confusion as you focus on the math.)
The solution to the quadratic equation is given by:
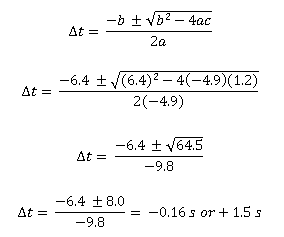
Note that the quadratic formula will always give you two solutions. Essentially, this is the formula for a full parabolic arc, and the two solutions will be the times that the object is at any given height in that arc (once going up, and once going back.) In this case, the ball was not thrown from the ground. If it had been thrown from the ground (at such a speed as to follow the same path,) it would have taken 0.16 s to get from the ground to your hand. It takes an additional 1.5 s to get from your hand back to the ground, which is the information that you want to find.
The acceleration of the ball (due to gravity) is downward, which is the negative y-direction as chosen in this problem. Because a, v, and y are all vector quantities, their values must be given a + or – sign to represent direction whenever they are filled into any of the kinematic equations.
Only two significant figures were given in the text of the problem, so only two significant figures are included in the solution.
Many of the most common mistakes in kinematic problems can be avoided with careful attention to book keeping. When we drew the picture, we were careful to label each point of interest with a different subscript, and when we fill into the equation we need to be careful to fill in the correct value for the correct point. We cannot assume that values of zero go with the earlier point in times. In this expression, in fact, the position y=0 occurs at the end of the motion (Point 3) rather than at the start (Point 1.)
Note that the quadratic formula will always give you two solutions. Essentially, this is the formula for a full parabolic arc, and the two solutions will be the times that the object is at any given height in that arc (once going up, and once going back.) In this case, the ball was not thrown from the ground. If it had been thrown from the ground (at such a speed as to follow the same path,) it would have taken 0.16 s to get from the ground to your hand. It takes an additional 1.5 s to get from your hand back to the ground, which is the information that you want to find.
How do you pick y = 0?
All that matters for describing motion is that you explicitly state where your reference point is. In this case, the problem gave heights relative to the ground, and so that is where I chose my reference point. If you picked the starting point (your hand) to be y = 0, then the ground would be at y = -1.2 m and y2 would be 2.1 m. You will get the same answers in either case.
Why did you draw the path of the ball as a parabola rather than showing it straight up and down?
This is just for convenience in showing all three points on the diagram. Point 3 really is directly below point 1.
My book uses “t” rather than “Δt” in the equations. Is that ok?
orMy book gives more than three equations. Why do you only use these three?
The t in the kinematic equations refers to the time interval between the two points in the equation, with y0 occurring at the earlier time. I use Δt rather than t to be explicit that this is a time interval (t - t0) and not a point in time.
Some text books will give more than three kinematic equations—for example, they may provide “range equations” or different versions of the equations for horizontal and vertical motion. Those are just these three equations solved for special cases. In my view, it is better to know and understand three equations that will always work than to memorize many equations which are specific to certain situations only.How did you know which two points to pick?
You are asked to find the amount of time the ball takes to get from Point 1 (when it leaves your hand) until it reaches the ground (Point 3.) Therefore, “y0” and “y” are “y1” and “y3” respectively.
Why is 9.8 m/s2 negative?
The acceleration of the ball (due to gravity) is downward, which is the negative y-direction as chosen in this problem. Because a, v, and y are all vector quantities, their values must be given a + or – sign to represent direction whenever they are filled into any of the kinematic equations.
Why is v2 0 instead of v1?
Many of the most common mistakes in kinematic problems can be avoided with careful attention to book keeping. When we drew the picture, we were careful to label each point of interest with a different subscript, and when we fill into the equation we need to be careful to fill in the correct value for the correct point. We cannot assume that values of zero go with the earlier point in times. In this expression, in fact, the position y=0 occurs at the end of the motion (Point 3) rather than at the start (Point 1.)
My numbers are close but not exactly what is shown in the equation. Am I close enough?
Only two significant figures were given in the text of the problem, so only two significant figures are included in the solution.
How did you know which two points to pick?
You are asked to find the amount of time the ball takes to get from Point 1 (when it leaves your hand) until it reaches the ground (Point 3.) Therefore, “y0” and “y” are “y1” and “y3” respectively.
Why is 9.8 m/s2 negative?
The acceleration of the ball (due to gravity) is downward, which is the negative y-direction as chosen in this problem. Because a, v, and y are all vector quantities, their values must be given a + or – sign to represent direction whenever they are filled into any of the kinematic equations.
Why is v3 0 instead of y1?
Many of the most common mistakes in kinematic problems can be avoided with careful attention to book keeping. When we drew the picture, we were careful to label each point of interest with a different subscript, and when we fill into the equation we need to be careful to fill in the correct value for the correct point. We cannot assume that values of zero go with the earlier point in times. In this expression, in fact, the position y=0 occurs at the end of the motion (Point 3) rather than at the start (Point 1.)
How did you solve for Δt?
To solve for Δt in this equation, recognize that you have a quadratic equation: it has the form a Δt2 + b Δt + c = 0, where a = -4.9, b = 6.4, and c = 1.2. (A quick look at units tells you that Δt must be in seconds, so I will not carry units through on the algebra to solve the quadratic equation, merely because I want to avoid confusion as you focus on the math.)
The solution to the quadratic equation is given by:
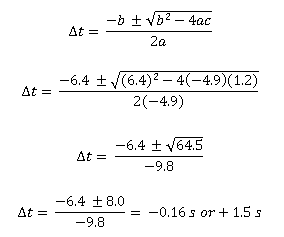
Note that the quadratic formula will always give you two solutions. Essentially, this is the formula for a full parabolic arc, and the two solutions will be the times that the object is at any given height in that arc (once going up, and once going back.) In this case, the ball was not thrown from the ground. If it had been thrown from the ground (at such a speed as to follow the same path,) it would have taken 0.16 s to get from the ground to your hand. It takes an additional 1.5 s to get from your hand back to the ground, which is the information that you want to find.
My numbers are close but not exactly what is shown in the equation. Am I close enough?
Only two significant figures were given in the text of the problem, so only two significant figures are included in the solution.
What is the acceleration of the ball? How do you know?
In this problem, you are explicitly told to ignore air resistance. (Even if you weren’t, air resistance on objects intended to be projectiles which are moving at low speeds is typically quite small.) Therefore, the only significant cause of the ball’s acceleration is gravity. For all objects near the Earth’s surface, the downward acceleration due to gravity, g, has a value of 9.8 m/s2. (If you have already studied forces, you can see this quickly with a free body diagram.)
How do you pick y = 0?
All that matters for describing motion is that you explicitly state where your reference point is. In this case, the problem gave heights relative to the ground, and so that is where I chose my reference point. If you picked the starting point (your hand) to be y = 0, then the ground would be at y = -1.2 m and y2 would be 2.1 m. You will get the same answers in either case.
The ball was thrown straight up. Why did you show it following a parabolic path?
This is just for convenience in showing all three points on the diagram. Point 3 really is directly below point 1.
My book uses variables like y, y0, v, v0, and t. Why do you use 1, 2 and 3 as subscripts, and Δt instead of t?
The kinematic equations relate position and velocity at any two points in the motion. Because many problems provide or ask about information at more than two points, I identify each point with its own subscript to keep them straight. I can then pick any two points to be y0 and y when I use the equations. The t in the kinematic equations refers to the time interval between the two points in the equation, with y0 occurring at the earlier time. I use Δt rather than t to be explicit that this is a time interval (t – t0) and not a point in time.
-

v22 = v12 + 2a(y2 – y1)
0 = v12 + 2(-9.8 m/s2)(3.3 m – 1.2 m)
v1 = 6.4 m/s
In this problem, you were first asked to find how fast you needed to throw the ball. In other words, you were asked to find the initial velocity of the ball. Because all equations include initial velocity, you could not use that as a criterion to select the best formula. However, you know that the ball reaches a maximum height (vy = 0 at the top of the motion) of 3.3 m, so the best relation to select is the one that relates position and velocity. The speed of 6.4 m/s is about 14 mph, so is a reasonable answer.
y3 = y1 + v1Δt + ½ a(Δt)2
0 = 1.2 m + (6.4 m/s) Δt + ½ (-9.8 m/s2)( Δt)2
Δt = -0.16 s or +1.5 s
Δt = 1.5 s
In part b), you were asked to find how long (time) it took the ball to reach the ground (position) and so the position-time equation was used between the initial and final locations. Because the position-time equation includes a ( Δt)2 term, it will always give two answers for time. The solution that makes physical sense is the positive time, or 1.5 s after the ball leaves your hand.
